Algorithmic worlds

Search blog posts

Next posts

2011-07-27 Announcements

2011-07-24 Down the rabbit hole

2011-07-17 Hubert Duprat

2011-07-15 Ashes and ice

2011-07-10 Inverted Julia

2011-06-19 New gigapixel image

2011-06-18 Giuseppe Randazzo

2011-05-24 Gigapixel images are back

2011-05-02 Dan Wills

2011-04-29 Barbara Takenaga

Previous posts

Blog

A blog about algorithmic art and fractal aesthetic. Click here to subscribe to the RSS feed.

July 10th 2011

Inverted Julia

The "Ducks" algorithm is attractive, because it produces patterns displaying dense fractal structures (they are fractal "everywhere"). Let me recall here its basic features. It involves performing two types of transformations on the complex plane. One is a folding operation that performs a symmetry about an axis in the plane. The second is a certain conformal transformation of the plane. The plane is then colored according to the orbits of the points under the iteration of these two transformations. The dense fractal pattern arises when the orbits of the points are chaotic. This arises only for certain choices of a parameter of the conformal transformation.

Due to the folding transformation, the resulting pattern possess many "local" mirror symmetries, that is symmetries that are not true symmetries of the whole pattern, but only symmetries of parts of the pattern. For instance, if you look at the bottom of 200110326-1 below, it seems there is a symmetry axis cutting almost vertically through the picture, but an examination of the top of the picture shows that this is not a true symmetry axis, the pattern is not symmetric up there.

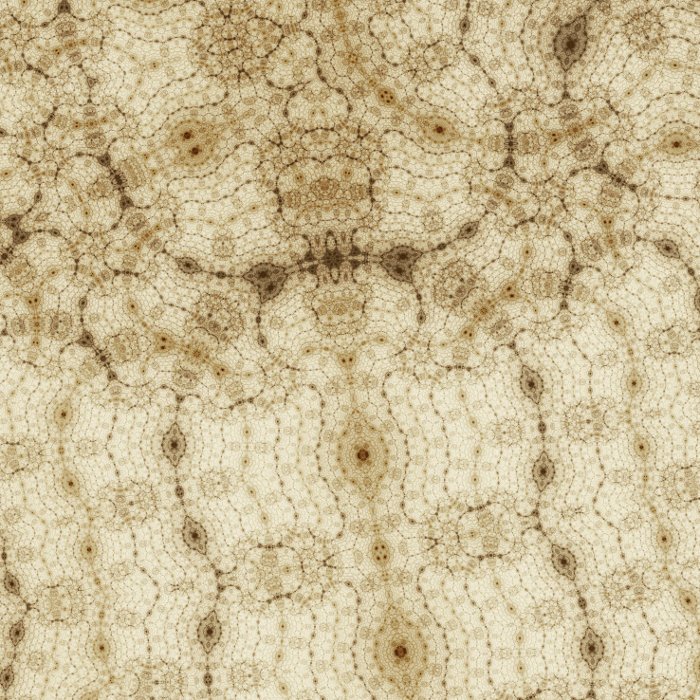
The fact that the folding transformation is 2 to 1 is crucial, as it relates different parts of the pattern two by two, what ultimately yields the self-similarity of the pattern. The precise form of the conformal transformation is not very important. There are mainly two requirement. The first is that it should really be a CONFORMAL transformation, that is a transformation that preserves angles. Non-conformal transformations tends to stretch the pattern, turning it into inaesthetic bundles of lines and hiding the fractal structure. Note that the folding transformation is itself almost conformal; it fails to be conformal only on the folding axis. The second requirement is that it should tends to keep the points at finite distance, in order to have a chance to get chaotic orbits. This was achieved in Ducks using a logarithm. But there are other possibilities, see for instance this thread on FractalForums. Fractal patterns obtained by different conformal transformation might have a slightly different aspect, but the main feature - the local mirror symmetries - remains.

Today I'd like to explain how to get radically different fractal patterns from the same idea. Clearly, in order to get rid of the local mirror symmetries, we should get rid of the folding transformation. From the discussion above, we should replace it by some 2 to 1 conformal or almost conformal transformation.

There is such a transformation. It is known to everyone in the fractal community: the square operation z -> z^2, used to draw the celebrated Mandelbrot and Julia sets. This transformation has a different type of symmetry: it is central-symmetric about a point, or equivalent symmetric under a 180 degree rotation. The Mandelbrot and Julia set do not have region of their parameter space where all the orbits are chaotic, so they do not display space-filling fractal patterns. To create a Ducks-like algorithm from it, one has to combine it with certain conformal transformations that yield chaotic orbits. We then get new types of space-filling patterns, displaying local central symmetry instead of mirror symmetry. The fact that they share the same symmetries as the Julia patterns make them very reminiscent of the latter. ([Update]: They are in fact very natural generalizations of the usual Julia sets, see this blog post!) Here is an example, 20110422-1:

For lack of a better name, I named the algorithm "Inverted Julia", because of some details of the algorithm. The following animated GIF shows the iterations of the algorithm, for the pattern of 20110422-1. Click here for a 500x500 pixel version of this animation (8MB).

Works using "Inverted Julia" have been collected here.